Las matemáticas ‘ocultas’ tras la Catedral de Burgos

Hace unas semanas resaltamos la importancia de la Alhambra en relación a la concepción musulmana de la geometría, y hoy nos acercaremos a otro lugar paradigmático como pocos: la catedral de Burgos.

Cualquiera que se haya acercado mínimamente a la construcción o a la reforma de una edificación, se percata de que por mucho que los planos y las mediciones digan una cosa, llevarlo a la realidad no es nada sencillo. Imaginémonos un edificio de las dimensiones de una catedral, y con los medios existentes en el siglo XIII, por no hablar de las sucesivas ampliaciones y añadidos que se hacen posteriormente que obligan a nuevos cálculos y una precisión exquisitos, si queremos que aquello perdure. Pero no sólo es la técnica, porque estos monumentos pretendían transmitir algo más que ser utilizadas como simples lugares de encuentro.

Para un mensaje trascendente, como sucede en el caso religioso, esta impresión se pensaba que se encontraba en aquello que transmitiera cualidades como la perfección, que siempre se asoció a la armonía y la belleza, y que a su vez se encuentran, por ejemplo, a través de la simetría, del orden. Todas estas características se perciben subjetivamente, pero se comprueban objetivamente haciendo cálculos y mediciones, matemáticas mediante.

En cada región de nuestro país, existen sociedades de profesores de matemáticas, tanto en activo como jubilados, que proponen actividades, organizan eventos, y en ocasiones analizan y realizan estudios e investigaciones. Este es el caso de la reciente publicación ‘Tesoros Matemáticos de la Catedral de Burgos‘, un magnífico y pormenorizado estudio editado por la Sociedad Castellana y Leonesa de Educación Matemática Miguel de Guzmán. A lo largo de nueve capítulos desgrana y, sobre todo, expone con mucha claridad, los innumerables aspectos matemáticos que este edificio atesora, y cuyo conocimiento aporta una nueva y complementaria dimensión a su historia y su arte, enriqueciendo y clarificando ambos. Tras una reflexión inicial sobre el significado interior de la catedral, y cómo la mirada matemática puede hacernos cambiar nuestra perspectiva tanto de la catedral como de las propias matemáticas, comienza un didáctico recorrido desde la capilla mayor y la cabecera, lugar desde el que se inició la construcción en 1221. Ya desde ahí aparecen las sorpresas: tres decágonos regulares (polígonos de diez lados) anidados (mismo centro y lados paralelos) conforman los espacios entre las capillas radiales, la girola y la capilla mayor; decágonos que además guardan una milimétrica proporción de separación en la que interviene phi, el número áureo, que marca el canon clásico de la belleza por excelencia.

Son varios los lugares en todo el monumento en que se presentan sucesiones de objetos geométricos anidados, que generan, según los arquitectos, euritmia, es decir, un movimiento armónico, que busca influir en el estado de ánimo del visitante. Esa euritmia se simula (obviamente la piedra no se mueve) mediante el encadenamiento de las proporciones, la repetición periódica de determinados patrones, la analogía. Estas repeticiones pretenden componer ritmos, acordes; por todo ello esta catedral es descrita a través de sus piedras como una sinfonía silenciosa. Diseminados por sus páginas se incluyen dieciséis códigos QR que nos llevan a animaciones que ilustran determinados conceptos. En concreto, esta descripción de los decágonos y las proporciones entre sus lados y las distancias entre los pasillos que dejan podemos verla perfectamente en este enlace.

El recorrido continúa por la Capilla de los Condestables, en cuyo estudio matemático se describe la vesica piscis (o vejiga de pez, zona común a dos circunferencias tales que el centro de cada una es un punto de la otra; es una configuración simbólica muy importante a lo largo de la historia, en la que, por ejemplo, en el Románico, se inserta el Pantocrátor). En la imagen, observamos las dos circunferencias de centros respectivos los puntos C y D y radios AD = AC. De esta igualdad se deduce que el triángulo ACD es equilátero y se cumple que

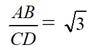
Este valor determina las proporciones en un triángulo equilátero y al ser un número irracional es una de las llamadas proporciones dinámicas, muy presentes en toda la historia del Arte. A modo de síntesis, cuando las proporciones (cociente entre largo y ancho de un elemento arquitectónico) son números racionales, se llaman estáticas, mientras que, si son números irracionales, se denominan dinámicas. En el siguiente cuadro se resumen las más habituales:

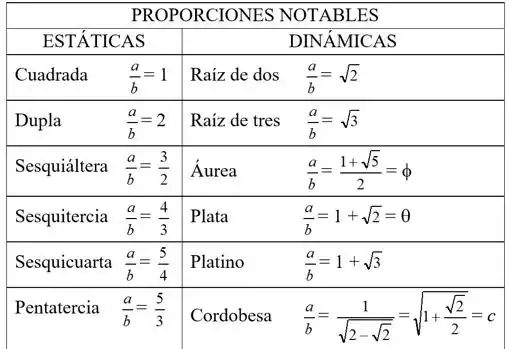
El capítulo incluye también un estudio de los frisos (repeticiones periódicas longitudinales de un mismo motivo, llamado módulo) y los siete tipos existentes, explicando una de sus nomenclaturas; también explica la presencia de octógonos y sus derivados estrellados junto con su indisociable proporción cordobesa.

A continuación, se realiza un pormenorizado análisis de uno de los elementos más representativos de la catedral burgalesa: las agujas. Como vemos en la primera imagen, esas agujas son pirámides de base octogonal, cuyas caras triangulares están ornamentadas con distintos tipos de tracerías de piedra, en nueve niveles (alturas) diferentes. Los maestros canteros pudieron haber utilizado el mismo motivo geométrico para todos esos niveles; sin embargo, no es así, y su riqueza y variedad quedan manifiestas haciendo un estudio y análisis geométrico-matemático.

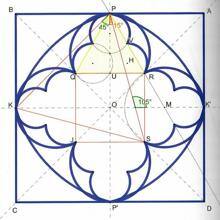
Por ejemplo, en el segundo nivel nos encontramos con la tracería de la imagen ampliada. ¿Cómo se ha construido? Traslademos ese modelo al papel mediante un software gráfico como Geogebra (de amplia difusión en nuestros centros educativos, y gratuito; además muy sencillo de manejar). A primera vista, tenemos unos arcos de circunferencia y unos lóbulos inscritos en ellas (cuatro, incluyendo a su vez cada uno otros tres), todo ello dentro del cuadrado ABCD, compuesto a su vez por cuatro cuadrados idénticos APOK’, PBKO, OKCP’ y K’OP’D (si cada uno de ellos tiene una longitud de lado a, el cuadrado ABCD tendrá por lado 2a). Con esa modelización, las coordenadas de todos los puntos mencionados son conocidas; el problema está en determinar las de R, Q, J y S.

Una condición adicional que podemos imponer para ello, es considerar que el triángulo PKS, señalado en color rojo, sea equilátero (lados iguales). Eso conlleva que sus ángulos sean de 60º, y como el ángulo KPO es por construcción de 45º, entonces el ángulo OPS tiene que ser de 15º, y por ello el ángulo que forma el lado PS con KK’ es de 105º (90º + 15º). Gracias a la trigonometría, tenemos entonces que la pendiente m del lado PS es

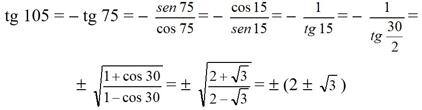
Tal y como tenemos situado el triángulo PKS, de los cuatro valores posibles el que resulta adecuado considerar es el correspondiente al segundo cuadrante, por lo que la ecuación del lado PKS (ecuación de la recta) es

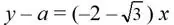
Finalmente, las coordenadas de S se obtienen resolviendo el sistema determinado por la ecuación anterior del lado PKS con la bisectriz del segundo cuadrante (en el dibujo la recta BD) de ecuación y = – x. De este modo, se obtiene que

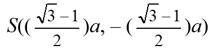
Y sería demasiada casualidad pensar que la aparición del número (sqrt(3)–1)/2, inverso de 1+sqrt(3), el número de platino, es por puro azar, ¿no les parece? Pero no es la única “sorpresa” que encontramos en esta tracería, porque en la búsqueda de las coordenadas de los vértices de los triángulos que dan lugar a los tréboles (arcos trilobulados) surgen relaciones combinadas entre sqrt(2) y sqrt(3), además de curiosas simetrías y propiedades de regularidad de los polígonos asociados, que no detallamos por no cansar al lector, al que remitimos al libro en cuestión para descubrir todos esos detalles.

Los restantes capítulos son, a cada cual más espectacular, gracias también a las precisas fotografías y fotogrametrías realizadas sobre ellas, abordando los arcos, los rosetones (explicando y analizando sus tipos y proporciones), el cimborrio (con un estudio casi exhaustivo del mismo), la escalera dorada, otro de los elementos más recordados y característicos de este edificio por su espectacularidad. Seguramente a ello contribuyen sus proporciones, además de su forma, ya que como podemos apreciar en la fotografía de la portada del libro incluida al inicio de este artículo, el número áureo, y la sucesión

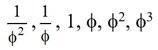
es claramente manifiesta, al igual que algunos de sus términos en otros lugares de la seo. Lo cierto es que las sorpresas son constantes. ¿Quién podría suponer, por ejemplo, que en algunos de los rosetones de la catedral de Burgos podríamos encontrar pétalos nazaríes (en la imagen, uno resaltado en color amarillo)? Esta construcción abunda en la Alhambra de Granada (de ahí el adjetivo que la define), y además verifica que

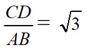
siendo su superficie idéntica a la de la vesica piscis. Es tan valiosa la información que todas estas construcciones aportan al entendimiento de la época de su construcción, que se está estudiando la posibilidad de incorporar a las visitas guiadas a la Catedral explicaciones de tipo matemático, lo que la convertiría probablemente en el primer edificio de Europa (quizá mundial) en disponer de esta peculiaridad.

El libro termina con una propuesta didáctica (no sólo para alumnos escolarizados sino para todo lector que quiera autoevaluarse respecto a todo lo descrito en las páginas precedentes, incluyéndose actividades dinámicas como entretenidos escape rooms). El grupo EstalMAT de Burgos ya editó en 2009 un recorrido didáctico por la catedral y viene realizando año tras año diferentes actividades en torno a las matemáticas y el arte. Algunas charlas han sido grabadas y están disponibles en la red.

La presencia de las matemáticas en disciplinas humanísticas es indiscutible, por mucho que a lo largo de los años se hayan tratado de separar (¿alguna vez dejaremos de escuchar aquello de «es que yo soy de letras»?). Autores como José Jiménez Lozano, premio Cervantes, resumía magistralmente lo que pretendía transmitir con esta reseña en su Guía espiritual de Castilla (1984): «La catedral es también una figura del saber: de las matemáticas y de la música o la astronomía, que, en el fondo, serían una sola cosa. Una construcción en el orden o unidad armónica, con la dialéctica, o razón razonable, que es la que une a todas. Las matemáticas han permitido incluso que las catedrales sean lo que son, gracias al arbotante y a la solución técnica de la bóveda de crucero. Los astros muestran un orden matemático y la música es una matemática armonía que la razón entiende; y esa armonía es, en lo que consiste la belleza».

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la Real Sociedad Matemática Española (RSME).

El ABCdario de las Matemáticas es una sección en colaboración con la RSME.

ABC de Madrid